Human-Centered Systems and Control Lab

We develop computationally efficient methods and theory for probabilistic safety, based in control, optimization, and non-parametric learning. Techniques we have developed have been applied to partially automated vehicles, aircraft flight management systems, space vehicles, and robotics.

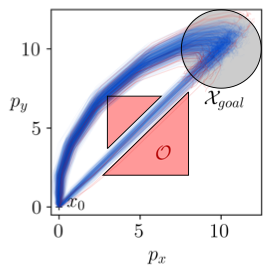
Data-driven stochastic optimal control

Kernel-based stochastic optimal control

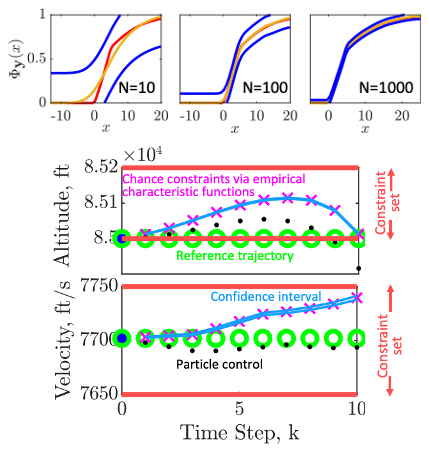
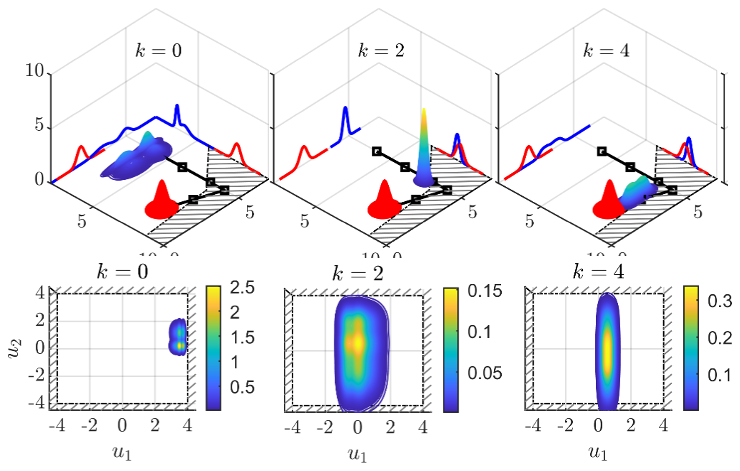
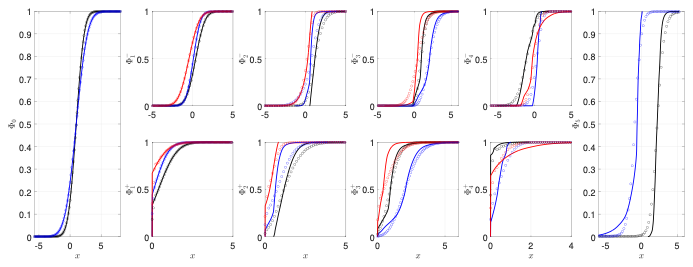
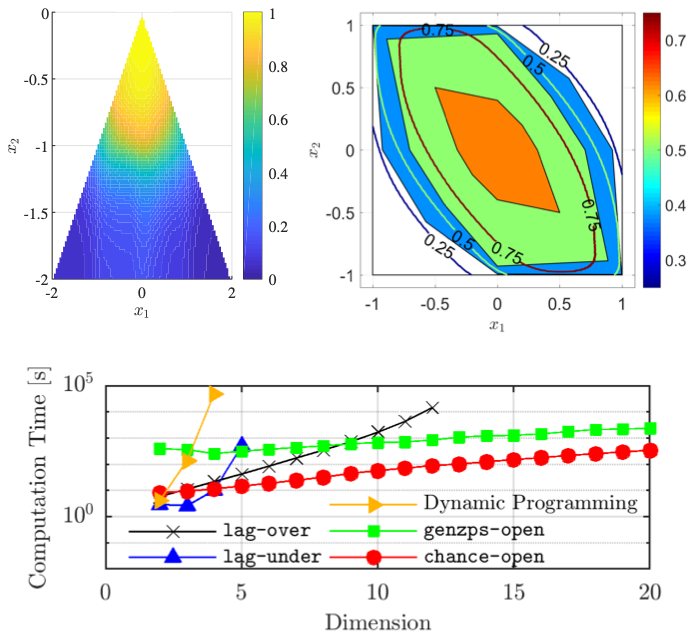
We use mathematical tools from functional analysis and statistical learning theory to solve data-driven stochastic optimal control problems Our methods are based in a non-parametric learning technique, conditional distribution embeddings, which exploit properties of reproducing kernel Hilbert spaces. This approach enables efficient controller synthesis, including via gradient descent and other methods, within the Hilbert space, that can be solved efficiently as a linear program.

Characterizing human heterogeneity in human-in-the-loop systems

Investigation of human driving characteristics plays a pivotal role for modeling and control of human-automation systems. As autonomy becomes pervasive, methods that can effectively characterize individual driver behavior will become paramount to ensure efficiency, safety, and high levels of performance. We have developed a non-parametric modeling framework based on kernel embeddings of distributions for the purpose of personalized characterization. Future work will incorporate such characterization for controller synthesis.

Group dynamics in learning environments

Understanding how to engage students in open-ended engineering design problems is a common problem for instructors of engineering. We utilize data-driven stochastic reachability techniques to analyze data on the agency and engagement of design students in group settings based on student conversations. We aim to enhance the understanding of instructors to enable teaching interventions to optimize student engagement.

Characterizing voids in laser deposition based additive manufacturing

Directed energy deposition (DED) is a laser and powder-based metal additive manu- facturing process with a high degree of variability between printed parts, even under identical manufacturing conditions. This process has proven difficult to control due to lack of accurate mathematical models to fully describe it. Our work in this area aims to enable future control of DED processes by using data-driven reachability analysis and neural networks to provide likelihood metrics of internal flaw formation in DED parts.

Chance constrained stochastic optimal control

Exploiting statistical properties for arbitrary stochastic disturbances

In many cases, non-Gaussian disturbances won't elicit closed form distributions when propagated through a system, making it difficult to synthe- size controllers with safety guarantees. We have developed methodologies that allow for controller synthesis with probabilistic safety guarantees when the disturbance fol- lows an arbitrary distribution to solve these problems. Methods have been developed based in the use of analytic and numerical quantiles, and analytic and sample computed moments

Characteristic functions

Stochastic optimal control for discrete time systems beyond the standard distribution assumptions prove to difficult to address for real world systems beyond Gaussians. Characteristic functions prove to be viable means of addressing these difficulties be addressing them in a Fourier space. We have been using characteristic functions in both stochastic optimal control and reachability in real-world problems with non-Gaussian uncertainty

Empirical Char Funs for Stoch Opt Control

Propagation of distributions through ReLU neural nets

Stochastic reachability

Probabilistic neural net verification

We seek to characterize neural nets in response to inputs represented by an entire distribution, as opposed to individual samples. We seek to predict output distributions and characterize the likelihood of the output staying within known, polytopic sets.

Stochastic reachability via characteristic functions

We solve for stochastic reachability likelihoods and level sets via convex optimization with stochastic cost, by exploiting log-concavity of the probability distribution function, linearity of the dynamics, and convexity of time-varying target sets.

Efficient propagation of probability distributions

We apply measure theoretic concepts to the stochastic reachability problem, such that for every initial probability measure, we seek to determine there exists an admissible of sequence of control actions that enforce the transition kernel almost surely.